Учебник. Относительность движения

Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.

Пусть имеются две системы отсчета. Система XOY условно считается неподвижной, а система X'O'Y' движется поступательно по отношению к системе XOY со скоростью ${\stackrel{⟶}{\upsilon }}_0$ Система XOY может быть, например, связана с Землей, а система X'O'Y' – с движущейся по рельсам платформой (рис. 1.2.1).

Сложение перемещений относительно разных систем отсчета

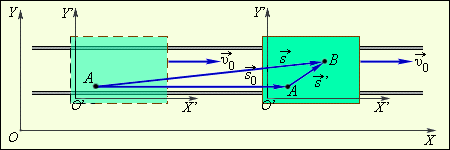
Пусть человек перешел по платформе за некоторое время из точки A в точку B. Тогда его перемещение относительно платформы соответствует вектору $\stackrel{⟶}{s}\mathrm{\text{'}}$ а перемещение платформы относительно Земли соответствует вектору ${\stackrel{⟶}{s}}_0$ Из рис. 1.2.1 видно, что перемещение человека относительно Земли будет соответствовать вектору $\stackrel{⟶}{s}$ представляющему собой сумму векторов ${\stackrel{⟶}{s}}_0$ и $\stackrel{⟶}{s}\mathrm{\text{'}}$ $\overrightarrow{s}={\overrightarrow{s}}_0+\overrightarrow{s}\mathrm{\text{'}}\mathrm{.}$

В случае, когда одна из систем отсчета движется относительно другой поступательно (как на рис. 1.2.1) с постоянной скоростью ${\overrightarrow{\upsilon }}_0\mathrm{,}$ это выражение принимает вид: $\overrightarrow{s}={\overrightarrow{\upsilon }}_0\Delta t+\overrightarrow{s}\mathrm{\text{'}}\mathrm{.}$

Если рассмотреть перемещение за малый промежуток времени Δt, то, разделив обе части этого уравнения на Δt и затем перейдя к пределу при Δt → 0 получим: $\overrightarrow{\upsilon }={\overrightarrow{\upsilon }}_0+\overrightarrow{\upsilon }\mathrm{\text{'}}\mathrm{.}$

Здесь $\overrightarrow{\upsilon }$ – скорость тела в «неподвижной» системе отсчета XOY, $\overrightarrow{\upsilon }$ – скорость тела в «движущейся» системе отсчета X'O'Y'. Скорости $\overrightarrow{\upsilon }$ и $\overrightarrow{\upsilon }$ иногда условно называют абсолютной и относительной скоростями; скорость ${\overrightarrow{\upsilon }}_0$ называют переносной скоростью.

Соотношение (*) выражает классический закон сложения скоростей:

Абсолютная скорость тела $\overrightarrow{\upsilon }$ равна векторной сумме его относительной скорости $\overrightarrow{\upsilon }$ и переносной скорости ${\overrightarrow{\upsilon }}_0$ движущейся системы отсчета.

Следует обратить внимание на вопрос об ускорениях тела в различных системах отсчета. Из (*) следует, что при равномерном и прямолинейном движении систем отсчета друг относительно друга ускорения тела в этих двух системах одинаковы, т. е. $\overrightarrow{a}=\overrightarrow{a}\mathrm{\text{'}}\mathrm{.}$ Действительно, если ${\overrightarrow{\upsilon }}_0$ – вектор, модуль и направление которого остаются неизменными во времени, то любое изменение $\mathrm{\Delta }\overrightarrow{\upsilon }\text{'}$ относительной скорости тела будет совпадать с изменением $\mathrm{\Delta }$ его абсолютной скорости. Следовательно, $\frac{\Delta \overrightarrow{\upsilon }}{\Delta t}$

Переходя к пределу (Δt → 0), получим $\overrightarrow{a}=\overrightarrow{a}\mathrm{\text{'}}\mathrm{.}$

В общем случае, при движениях систем отсчета с ускорением друг относительно друга, ускорения тела в различных системах отсчета оказываются различными.

В случае, когда вектора относительной скорости $\overrightarrow{\upsilon }$ и переносной скорости ${\overrightarrow{\upsilon }}_0$ параллельны друг другу, закон сложения скоростей можно записать в скалярной форме: υ = υ₀ + υ'.

В этом случае все движения происходят вдоль одной прямой линии (например, оси OX). Скорости υ, υ₀ и υ' нужно рассматривать как проекции абсолютной, переносной и относительной скоростей на ось OX. Они являются величинами алгебраическими и, следовательно, им нужно приписывать определенные знаки (плюс или минус) в зависимости от направления движения.