Учебник. Закон Био-Савара. Теорема о циркуляции *)

Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции:

Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.

Индукцию $\overrightarrow{B}$ проводника с током можно представить как векторную сумму элементарных индукций $\Delta \overrightarrow{B}\mathrm{,}$ создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад $\Delta \overrightarrow{B}$ в магнитную индукцию $\overrightarrow{B}$ результирующего магнитного поля, создаваемый малым участком Δl проводника с током I. $\Delta B=\frac{{\mu }_{0}I\Delta lsin\alpha }{4\pi r^2}\mathrm{.}$

Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ₀ – магнитная постоянная. Направление вектора $\Delta \overrightarrow{B}$ определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока: $B=\frac{{\mu }_0}{2\pi }\frac{I}{R}\mathrm{,}$ которая уже приводилась в § 1.16.

Иллюстрация закона Био–Савара

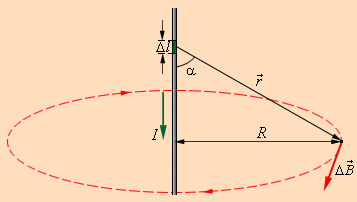
Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле $B=\frac{{\mu }_0}{2}\frac{I}{R}\mathrm{,}$ где R – радиус кругового проводника. Для определения направления вектора $\overrightarrow{B}$ также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.

Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользаоваться теоремой о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике.

Поясним понятие циркуляции вектора $\overrightarrow{B}\mathrm{.}$ Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую $B_l$ вектора $\overrightarrow{B}$ в данном месте, то есть определить проекцию вектора $\overrightarrow{B}$ на направление касательной к данному участку контура (рис. 1.17.2).

Замкнутый контур (L) с заданным направлением обхода. Изображены токи I₁, I₂ и I₃, создающие магнитное поле

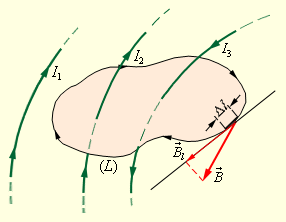
Циркуляцией вектора $\overrightarrow{B}$ называют сумму произведений $B_l$ Δl, взятую по всему контуру L: $\mathrm{Циркуляция вектора }\overrightarrow{B}=\sum _{\mathrm{(}L\mathrm{)}}{B}_l\Delta l\mathrm{.}$

Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура.

Теорема о циркуляции утверждает, что циркуляция вектора $\overrightarrow{B}$ магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ₀ на сумму всех токов, пронизывающих контур: $\sum _{\mathrm{(}L\mathrm{)}}{B}_l\mathrm{ \Delta }l={\mu }_0\sum I_i\mathrm{.}$

В качестве примера на рис. 1.17.2 изображены несколько проводников с токами, создающими магнитное поле. Токи I₂ и I₃ пронизывают контур L в противоположных направлениях, им должны быть приписаны разные знаки – положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно, I₃ > 0, а I₂ < 0. Ток I₁ не пронизывает контур L.

Теорема о циркуляции в данном примере выражается соотношением: $\sum _{\mathrm{(}L\mathrm{)}}{B}_l\mathrm{ \Delta }l={\mu }_0\mathrm{(}{I}_3-I_2\mathrm{)}\mathrm{.}$

Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции.

Простейшим примером применения теоремы о циркуляции является вывод формулы для магнитной индукции поля прямолинейного проводника с током. Учитывая симметрию в данной задаче, контур L целесообразно выбрать в виде окружности некоторого радиуса R, лежащей в перпендикулярной проводнику плоскости. Центр окружности находится в некоторой точке проводника. В силу симметрии вектор $\overrightarrow{B}$ направлен по касательной $\mathrm{(}$ , а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению: $\sum _{\mathrm{(}L\mathrm{)}}{B}_l\mathrm{ \Delta }l=2\pi RB={\mu }_{0}I\mathrm{,}$ откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током, приведенная ранее.

Этот пример показывает, что теорема о циркуляции вектора магнитной индукции $\overrightarrow{B}$ может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.

Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки (рис. 1.17.3).

Применение теоремы о циркуляции к тороидальной катушке

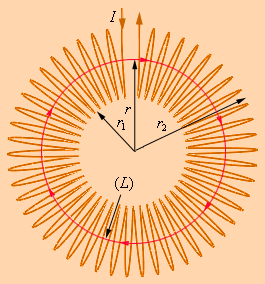
Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r₁ ≤ r < r₂ изображена на рис. 1.17.3. Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с изображенной на рис. 1.17.3 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора $\overrightarrow{B}$ одинаков вдоль всей этой линии. По теореме о циркуляции можно записать: B ċ 2πr = μ₀IN, где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно, $B=\frac{{\mu }_{0}IN}{2\pi r}\mathrm{.}$

Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r₂ – r₁ << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае B = μ ₀I n.

В это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами. Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки.

На рис. 1.17.4 изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри него.

Магнитное поле катушки конечной длины. В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки

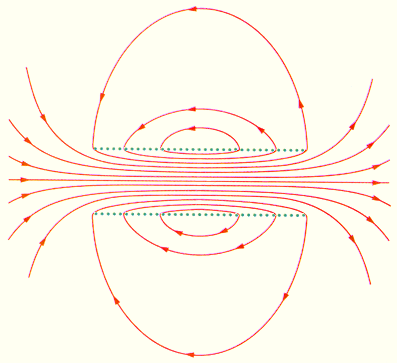
В случае бесконечно длинного соленоида выражение для модуля магнитной индукции можно получить непосредственно с помощью теоремы о циркуляции, применив ее к прямоугольному контуру, показанному на рис. 1.17.5.

Применение теоремы о циркуляции к расчету магнитного поля бесконечно длинного соленоида

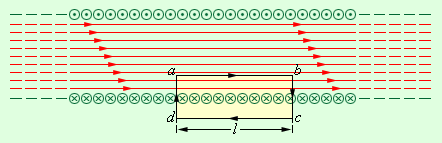
Вектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора $\overrightarrow{B}$ по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n ċ l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен I n l. Согласно теореме о циркуляции, B l = μ₀I n l, откуда B = μ₀ I n.

Это выражение совпадает с полученной ранее формулой для магнитного поля тонкой тороидальной катушки.