Учебник. Элементы релятивисткой динамики

Принцип относительности Эйнштейна утверждает инвариантность всех законов природы по отношению к переходу от одной инерциальной системе отсчета к другой. Это значит, что все уравнения, описывающие законы природы, должны быть инвариантны относительно преобразований Лоренца. К моменту создания СТО теория, удовлетворяющая этому условию, уже существовала – это электродинамика Максвелла. Однако уравнения классической механики Ньютона оказались неинвариантными относительно преобразований Лоренца, и поэтому СТО потребовала пересмотра и уточнения законов механики.

В основу такого пересмотра Эйнштейн положил требования выполнимости закона сохранения импульса и закона сохранения энергии в замкнутых системах. Для того, чтобы закон сохранения импульса выполнялся во всех инерциальных системах отсчета, оказалось необходимым изменить определение импульса тела. Вместо классического импульса $\stackrel{⟶}{p}=m\stackrel{⟶}{\upsilon }$ в СТО релятивистский импульс $\stackrel{⟶}{p}$ тела с массой m, движущегося со скоростью $\stackrel{⟶}{\upsilon }$ записывается в виде $\stackrel{⟶}{p}=\frac{m\stackrel{⟶}{\upsilon }}{\sqrt{1-{\upsilon }^2/c^2}}=\frac{m\stackrel{⟶}{\upsilon }}{\sqrt{1-{\beta }^2}}\mathrm{.}$

Если принять такое определение, то закон сохранения суммарного импульса взаимодействующих частиц (например, при соударениях) будет выполняться во всех инерциальных системах, связанных преобразованиями Лоренца. При β → 0 релятивистский импульс переходит в классический. Масса m, входящая в выражение для импульса, есть фундаментальная характеристика частицы, не зависящая от выбора инерциальной системы отсчета, а, следовательно, и от скорости ее движения. (Во многих учебниках прошлых лет ее было принято обозначать буквой m₀ и называть массой покоя. Кроме того, вводилась так называемая релятивистская масса, равная $m_0/\sqrt{1-{\beta }^2}\mathrm{,}$ зависящая от скорости движения тела. Современная физика постепенно отказывается от этой терминологии).

Основной закон релятивистской динамики материальной точки записывается так же, как и второй закон Ньютона: $\stackrel{⟶}{F}=\frac{d\overrightarrow{p}}{dt}\mathrm{,}$ но только в СТО под $\overrightarrow{p}$ понимается релятивистский импульс частицы. Следовательно, $\overrightarrow{F}=\frac{d}{dt}\left(\frac{m\overrightarrow{\upsilon }}{\sqrt{1-{\upsilon }^2/c^2}}\right)\mathrm{.}$

Так как релятивистский импульс не пропорционален скорости частицы, скорость его изменения не будет прямо пропорциональна ускорению. Поэтому постоянная по модулю и направлению сила не вызывает равноускоренного движения. Например, в случае одномерного движения вдоль оси x ускорение частицы $a=\frac{d\upsilon }{dt}$ под действием постоянной силы оказывается равным $a=\frac{F}{m}{\left(1-\frac{{\upsilon }^2}{c^2}\right)}^{\frac{3}{2}}\mathrm{.}$

Если скорость классической частицы беспредельно растет под действием постоянной силы, то скорость релятивистской частицы не может превысить скорость света c в пустоте. В релятивистской механике, так же, как и в механике Ньютона, выполняется закон сохранения энергии. Кинетическая энергия тела E_k определяется через работу внешней силы, необходимую для сообщения телу заданной скорости. Чтобы разогнать частицу массы m из состояния покоя до скорости υ₀ под действием постоянной силы F, эта сила должна совершить работу $A=\int Fċdx=\int Fċ\upsilon ċdt=\int \frac{\mathrm{m }\mathrm{a }\mathrm{\upsilon }dt}{{\left(1-{\upsilon }^2/c^2\right)}^{3/2}}\mathrm{.}$

Поскольку a dt = dυ, окончательно можно записать $E_{\mathrm{k}}=A=\underset{0}{\overset{{\upsilon }_0}{\int }}\frac{m\mathrm{ \upsilon }d\upsilon }{{\mathrm{(}1-{\upsilon }^2/c^2\mathrm{)}}^{3/2}}\mathrm{.}$

Вычисление этого интеграла приводит к следующему выражению для кинетической энергии (индекс «ноль» при скорости υ опущен): $E_{\mathrm{k}}=\frac{m{c}^2}{\sqrt{1-{\upsilon }^2/c^2}}-m{c}^2\mathrm{.}$

Эйнштейн интерпретировал первый член в правой части этого выражения как полную энергию E движущийся частицы, а второй член как энергию покоя E₀: $E=\frac{m{c}^2}{\sqrt{1-{\upsilon }^2/c^2}}\mathrm{,}$ E₀ = mc².

Кинетическая энергия E_k релятивистской динамики есть разность между полной энергией E тела и его энергией покоя E₀: E_k = E – E₀.

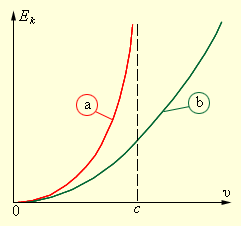
Рис. 4.5.1 иллюстрирует изменение кинетической энергии частицы в зависимости от ее скорости для частиц, подчиняющихся классическому и релятивистскому законам.

Зависимость кинетической энергии от скорости для релятивистской (a) и классической (b) частиц. При υ << c оба закона совпадают

Чрезвычайно важный вывод релятивистской механики заключается в том, что находящаяся в покое масса m содержит огромный запас энергии. Это утверждение имеет разнообразные практические применения, включая использование ядерной энергии. Если масса частицы или системы частиц уменьшилась на Δm, то при этом должна выделиться энергия ΔE = Δm ċ c². Многочисленные прямые эксперименты дают убедительные доказательства существования энергии покоя. Первое экспериментальное подтверждение правильности соотношения Эйнштейна, связывающего массу и энергию, было получено при сравнении энергии, высвобождающейся при радиоактивном распаде, с разностью масс исходного ядра и конечных продуктов. Например, при бета-распаде свободного нейтрона появляется протон, электрон и еще одна частица с нулевой массой – антинейтрино: $\mathrm{n}\to \mathrm{p}+{\mathrm{e}}^{\mathrm{-}}+\tilde{\nu }$

При этом суммарная кинетическая энергия конечных продуктов равна 1,25ċ10^–13 Дж. Масса нейтрона превышает суммарную массу протона и электрона на Δm = 13,9ċ10^–31 кг. Такому уменьшению массы должна соответствовать энергия ΔE = Δm ċ c² = 1,25ċ10^–13 Дж, равная наблюдаемой кинетической энергией продуктов распада.

Чтобы возникло ощущение масштабов этого явления в макромире, рассмотрим такой пример. При взрыве 1 т тринитротолуола высвобождается энергия 4,2ċ10⁹ Дж. При взрыве мегатонной бомбы выделится энергия 4,2ċ10¹⁵ Дж. Соответствующая этой громадной энергии масса m = E / c² оказывается равной всего 46 г. Таким образом, при взрыве ядерной мегатонной бомбы масса ядерной «взрывчатки» должна уменьшится примерно на 50 г. Полная первоначальная масса водородной бомбы, эквивалентной по мощности 1 мегатонне тринитротолуола, примерно в 1000 раз больше и составляет около 50 кг.

Закон пропорциональности массы и энергии является одним из самых важных выводов СТО. Масса и энергия являются различными свойствами материи. Масса тела характеризует его инертность, а также способность тела вступать в гравитационное взаимодействие с другими телами. Важнейшим свойством энергии является ее способность превращаться из одной формы в другую в эквивалентных количествах при различных физических процессах – в этом заключается содержание закона сохранения энергии. Пропорциональность массы и энергии является выражением внутренней сущности материи. Формула Эйнштейна E₀ = mc² выражает фундаментальный закон природы, который принято называть законом взаимосвязи массы и энергии.

Комбинируя выражение (*) для релятивистского импульса $\overrightarrow{p}$ и выражение (**) для полной энергии E, можно получить соотношение, связывающее эти величины. Для этого удобно формулы (*) и (**) переписать в следующем виде: ${\left(\frac{p^2}{mc}\right)}^2=\frac{{\upsilon }^2/c^2}{1-{\upsilon }^2/c^2}\mathrm{,}$ ${\left(\frac{E}{m{c}^2}\right)}^2=\frac{1}{1-{\upsilon }^2/c^2}\mathrm{.}$

Вычитая почленно, можно получить E² = (mc²)² + (pc)².

Отсюда еще раз следует, что для покоящихся частиц (p = 0) E = E₀ = mc².

Полученное соотношение показывает, что частица может иметь энергию и импульс, но не иметь массы (m = 0). Такие частицы называются безмассовыми. Для безмассовых частиц связь между энергией и импульсом выражается простым соотношением E = pc.

К безмассовым частицам относятся фотоны – кванты электромагнитного излучения и, возможно, нейтрино. Безмассовые частицы не могут существовать в состоянии покоя, во всех инерциальных системах отсчета они движутся с предельной скоростью c.