

 |
 |
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через 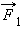 и
и 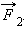 По третьему закону Ньютона
По третьему закону Ньютона 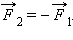 Если эти тела взаимодействуют в течение времени
Если эти тела взаимодействуют в течение времени 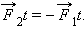 Применим к этим телам второй закон Ньютона:
Применим к этим телам второй закон Ньютона:
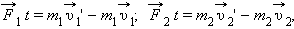 |
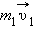 и
и 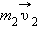 – импульсы тел в начальный момент времени,
– импульсы тел в начальный момент времени, 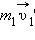 и
и 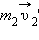 – импульсы тел в конце взаимодействия. Из этих соотношений следует:
– импульсы тел в конце взаимодействия. Из этих соотношений следует:
|
Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.
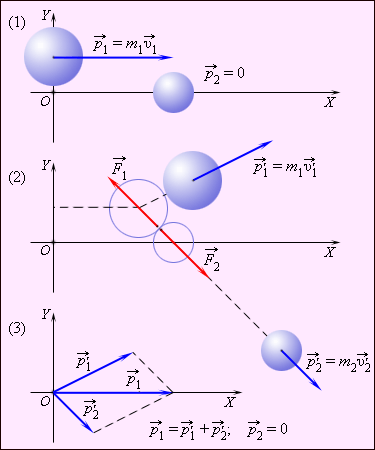
Рис. 1.17.1 иллюстрирует закон сохранения импульса на примере нецентрального соударения двух шаров разных масс, один из которых до соударения находился в состоянии покоя.
|
| Рисунок 1.17.1. Нецентральное соударение шаров разных масс: 1 – импульсы до соударения; 2 – импульсы после соударения; 3 – диаграмма импульсов |
Изображенные на рис. 1.17.1 вектора импульсов шаров до и после соударения можно спроектировать на координатные оси 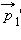 и
и 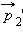 импульсов обоих шаров после соударения на ось
импульсов обоих шаров после соударения на ось
Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.
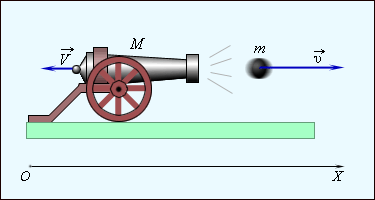
При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс (рис. 1.17.2). Если скорости орудия и снаряда обозначить через 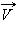 и
и 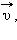 а их массы через
а их массы через
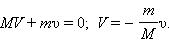 |
|
| Рисунок 1.17.2. Отдача при выстреле из орудия |
На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью 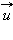 относительно ракеты. Обозначим массу выброшенных газов через
относительно ракеты. Обозначим массу выброшенных газов через
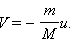 |
Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.
Для получения точной формулы процесс истечения газа из сопла ракеты нужно рассмотреть более детально. Пусть ракета в момент времени 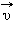 (рис. 1.17.3 (1)). В течение малого промежутка времени
(рис. 1.17.3 (1)). В течение малого промежутка времени 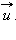 Ракета в момент
Ракета в момент 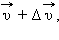 а ее масса станет равной
а ее масса станет равной 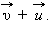 Применим закон сохранения импульса. В момент времени
Применим закон сохранения импульса. В момент времени 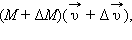 а импульс испущенных газов равен
а импульс испущенных газов равен 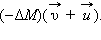 В момент времени
В момент времени 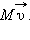 Предполагая систему «ракета + газы» замкнутой, можно записать:
Предполагая систему «ракета + газы» замкнутой, можно записать:
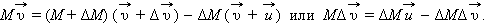 |
Величиной 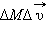 можно пренебречь, так как
можно пренебречь, так как
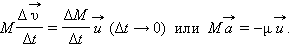 |
Величина 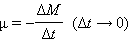 есть расход топлива в единицу времени. Величина
есть расход топлива в единицу времени. Величина 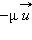 называется реактивной силой тяги
называется реактивной силой тяги 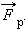 Реактивная сила тяги действует на ракету со стороны истекающих газов, она направлена в сторону, противоположную относительной скорости. Соотношение
Реактивная сила тяги действует на ракету со стороны истекающих газов, она направлена в сторону, противоположную относительной скорости. Соотношение
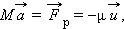 |
|
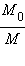 – отношение начальной и конечной масс ракеты. Эта формула называется формулой Циолковского. Из нее следует, что конечная скорость ракеты может превышать относительную скорость истечения газов. Следовательно, ракета может быть разогнана до больших скоростей, необходимых для космических полетов. Но это может быть достигнуто только путем расхода значительной массы топлива, составляющей большую долю первоначальной массы ракеты. Например, для достижения первой космической скорости
– отношение начальной и конечной масс ракеты. Эта формула называется формулой Циолковского. Из нее следует, что конечная скорость ракеты может превышать относительную скорость истечения газов. Следовательно, ракета может быть разогнана до больших скоростей, необходимых для космических полетов. Но это может быть достигнуто только путем расхода значительной массы топлива, составляющей большую долю первоначальной массы ракеты. Например, для достижения первой космической скорости 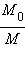 должно быть равно
должно быть равно 
 |
|
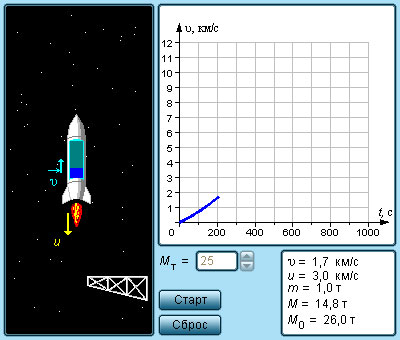
Модель.
Реактивное движение
|
Значительное снижение стартовой массы ракеты может быть достигнуто при использовании многоступенчатых ракет, когда ступени ракеты отделяются по мере выгорания топлива. Из процесса последующего разгона ракеты исключаются массы контейнеров, в которых находилось топливо, отработавшие двигатели, системы управления и т. д. Именно по пути создания экономичных многоступенчатых ракет развивается современное ракетостроение.
 |
 |
 |


Главная Бесплатные онлайн учебники Бесплатная подготовка по всем предметам онлайн |
||
|
© Физикон, 1999-2025 E-mail: |
||
|
|
||