

 |
 |
Прежде всего, на основе вашего поурочного плана определите, какие компьютерные модели вы сможете использовать при объяснении нового материала и/или предложить учащимся для работы в компьютерном классе. Для этой цели вам также может оказаться полезной информация, размещенная в следующем параграфе: «Модели компьютерного курса в программе по физике для 10 класса».
Далее имеет смысл к каждой выбранной модели составить таблицу, в которую следует занести названия параметров, которые может изменять пользователь, обозначения этих параметров, пределы и шаг их изменения. В эту таблицу также следует занести аналогичную информацию о параметрах модели, которые рассчитываются компьютером при выполнении экспериментов, и выводятся на экран монитора. Для создания такой таблицы нужно открыть соответствующую модель, определить диапазоны изменения регулируемых параметров, а затем провести несколько опытов с крайними значениями этих параметров. Такие эксперименты позволят вам определить предельные значения и шаг расчёта параметров, которые рассчитываются компьютером в ходе экспериментов.
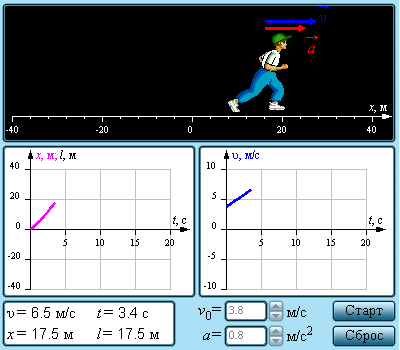
Рассмотрим в качестве примера компьютерную модель «Равноускоренное движение тела».
|
| Рисунок H.3.7.1. Вид окна модели «Равноускоренное движение тела» |
Поработав несколько минут с указанной моделью, вы сможете составить таблицу её параметров. Примерный вид такой таблицы показан ниже.
| Регулируемые параметры модели | |||
| Название | Обозначение | Пределы изменения | Шаг |
| Начальная скорость | от –5,0 до 5,0 м/c | 0,1 | |
| Ускорение | от –1,0 до 1,0 м/c2 | 0,01 | |
| Рассчитываемые параметры модели | |||
| Время | от 0 до 2000 с | 1 | |
| Скорость | от –1,0 до 6,2 м/с | 0,1 | |
| Координата | Г | от –200 до 200 | 0,05 |
| Координата | от 0 до 300 | 0,05 | |
При работе с любой моделью аналогичная таблица совершенно необходима для планирования экспериментов и составления заданий, так как, в отличие от персонального компьютера, может быть всегда под рукой.
| № | Начальная скорость |
Ускорение |
Время |
Текущая скорость |
Координата |
Путь |
| Равномерное движение | ||||||
| 1. | 0,5 | – | 200 | 0,5 | 100 | 200 |
| 2. | –0,4 | – | 100 | –0,4 | –40 | 40 |
| 3. | 0,8 | – | 50 | 0,8 | 40 | 40 |
| 4. | –0,6 | – | 40 | –0,6 | –24 | 24 |
| Равноускоренное движение | ||||||
| 5. | 0,0 | 0,1 | 50 | 5 | 125 | 125 |
| 6. | 1,0 | –0,1 | 10 | 0 | 5,0 | 5,0 |
| 7. | 1,0 | –0,1 | 20 | –1,0 | 0,0 | 10 |
| 8. | 0,5 | 0,05 | 60 | 3,5 | 120 | 120 |
| 9. | –0,5 | 0,05 | 40 | 1,5 | 1,5 | 25 |
| 10. | 0,4 | –0,01 | 80 | –0,4 | 0,0 | 16 |
Для заполнения, как таблиц, так и матриц можно привлечь слабых учеников, которым более сложные задания, например, по решению задач с компьютерной проверкой, явно не по силам. Как показывает опыт, слабые ученики с большим энтузиазмом выполняют эксперименты, хотя бы и однотипные, хорошо осваивают модели и впоследствии даже могут придумать и сформулировать собственные задачи. Такая работа оказывается чрезвычайно полезной как для самих учеников, так и для учителя, так как существенно экономит его время.
На основании любой строки матрицы можно сформулировать несколько задач. Отметим, что в качестве расчётных задач с последующей компьютерной проверкой предпочтительнее, так называемые, обратные задачи. Дело в том, что ответы к прямым задачам некоторые учащиеся предпочитают получать, установив значения числовых параметров модели в соответствии с условием задачи и поставив эксперимент. После получения ответа решать задачу им, как правило, уже неинтересно. Разумеется, и обратную задачу учащиеся могут пытаться «решать» экспериментальным путём, подбирая числовые значения параметров и ставя эксперименты. Однако, это занятие более длительное и не столь привлекательное, так как требует значительного количества однотипных экспериментов и не всегда приводит к нужному результату. В то же время, если задача на бумаге решена правильно и первый же эксперимент согласуется с ответом, учащиеся получают моральное удовлетворение гораздо большее, чем от ответа, полученного обманным путём. По указанной выше причине прямые задачи лучше давать в виде экспериментальных задач или заданий.
Приведём примеры прямых и обратных задач к модели «Равноускоренное движение тела», составленных с использованием выше приведенной матрицы.
Равномерное движение
Равноускоренное движение
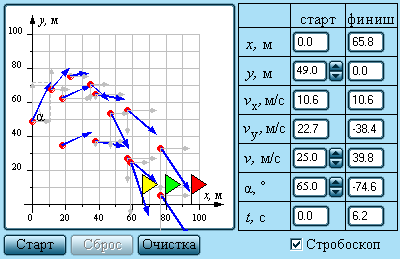
Приведём также в качестве примера таблицу параметров для компьютерной модели «Движение тела, брошенного под углом к горизонту».
|
Вид окна модели «Движение тела, брошенного под углом к горизонту» |
|
||||||||||||||||||||||||||||||||||||||||||||
Параметры модели «Движение тела, брошенного под углом к горизонту» |
||||||||||||||||||||||||||||||||||||||||||||
Из таблицы видно, что данную модель можно применять при изучении следующих видов движения:
Надеемся, что читателю уже понятно как составить матрицу с числовыми параметрами и сформулировать задачи на её основе. Мы же приведём в данном случае несколько задач из широко известного школьного задачника А. П. Рымкевича 1996 г. (в скобках указаны номера задач по задачнику 1988 г. издания), которые можно использовать при работе с данной моделью.
Из приведённых примеров видно, что с использованием модели «Движение тела, брошенного под углом к горизонту» можно проиллюстрировать самые разнообразные задачи.
Возможно, у вас, уважаемый терпеливый читатель, возникли законные вопросы: «Зачем такие сложности? К чему эти таблицы и матрицы? Почему бы ни сесть просто за компьютер, открыть нужную модель, и немного с ней поэкспериментировав, подготовить несколько задач или демонстрационных опытов?». Конечно, если вы только начинаете работать с «Открытой Физикой», и предполагаете при объяснении материала показать несколько опытов или провести пробный фрагмент урока в компьютерном классе, то так и следует сделать. Автор ещё помнит, что и сам начинал подобным образом. Однако, если вы нацелены на серьёзную и длительную работу с курсом, а ведь только так можно добиться существенного учебного эффекта, то без описанных выше «сложностей» вам не обойтись. На самом деле (вскоре вы в этом убедитесь) описанные приёмы только облегчат вашу работу и сэкономят уйму времени. Представьте себе, что неожиданно интересная идея по использованию модели на уроке возникла у вас на очередном педсовете, на котором обсуждаются проблемы информатизации учебного процесса, или в другой ситуации, когда компьютер или диск с курсом недоступны. Если же вы вникли в содержание модели, то одного беглого взгляда на таблицу с параметрами вам будет достаточно, чтобы понять, можно ли использовать модель в интересующих вас целях. Матрица же поможет вам составить любое, осуществимое в рамках модели, задание или лабораторную работу. Кроме того, раз уж авторы компьютерного курса создали такие замечательные модели, то почему бы ни использовать предоставленные возможности полностью, а в этом случае без описанных выше приёмов вряд ли можно обойтись.
 |
 |
 |


Главная Бесплатные онлайн учебники Бесплатная подготовка по всем предметам онлайн |
||
|
© Физикон, 1999-2026 E-mail: |
||
|
|
||