

 Задачи с решениями
Задачи с решениями

По круглому витку радиуса
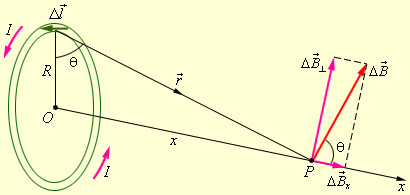
Задача решается с помощью закона Био–Савара. Разобьем виток с током на малые элементы 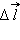 (см. рисунок).
(см. рисунок).
 |
Элемент 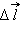 создает в точке
создает в точке 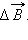 Модуль вектора
Модуль вектора 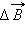 по закону Био–Савара равен:
по закону Био–Савара равен:
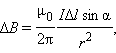
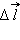 до точки
до точки 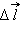 и
и 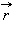 . В данном случае
. В данном случае 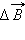 определяется правилом буравчика: оно совпадает с направлением вращения рукоятки воображаемого буравчика при его поступательном перемещении вдоль тока.
определяется правилом буравчика: оно совпадает с направлением вращения рукоятки воображаемого буравчика при его поступательном перемещении вдоль тока.
Вектор 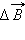 можно разложить на две составляющие:
можно разложить на две составляющие:
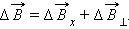
Составляющая 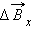 направлена вдоль оси витка, составляющая
направлена вдоль оси витка, составляющая 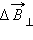 направлена перпендикулярно оси. При определении результирующего магнитного поля, создаваемого всеми элементами кольцевого тока, составляющие
направлена перпендикулярно оси. При определении результирующего магнитного поля, создаваемого всеми элементами кольцевого тока, составляющие 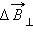 различных элементов в силу осевой симметрии задачи взаимно компенсируются. Составляющие
различных элементов в силу осевой симметрии задачи взаимно компенсируются. Составляющие
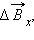 создаваемые различными элементами кольцевого тока, складываются и создают результирующее магнитное поле
создаваемые различными элементами кольцевого тока, складываются и создают результирующее магнитное поле 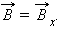
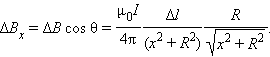
Переходом к пределу при
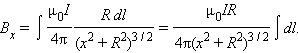
Интеграл по
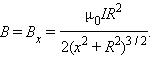
Обратим внимание, что направление результирующего вектора 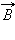 также может быть определено с помощью правила правого буравчика: если вращать рукоятку буравчика в направлении тока в кольце, то направление поступательного перемещения буравчика укажет направление индукции магнитного поля.
также может быть определено с помощью правила правого буравчика: если вращать рукоятку буравчика в направлении тока в кольце, то направление поступательного перемещения буравчика укажет направление индукции магнитного поля.
При
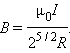
Подстановка числовых данных
Магнитное поле
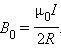
В условиях задачи
 1 из 2
1 из 2
 |