

 Задачи с решениями
Задачи с решениями

Электрический заряд 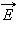 в точке
в точке
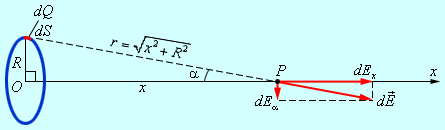
Общий прием решения задач по определению электрического поля непрерывного распределения зарядов состоит в разбиении заряженного тела на элементарные объемы, размер которых много меньше расстояния до точки наблюдения. Электрическое поле зарядов, попавших в элементарные объемы, может быть найдено по закону Кулона. Полное поле находится по принципу суперпозиции как векторная сумма элементарных полей.
Рассмотрим малый элемент 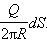 Модуль вектора напряженности электрического поля, создаваемого зарядом
Модуль вектора напряженности электрического поля, создаваемого зарядом
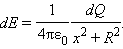
Составляющая этого поля вдоль оси
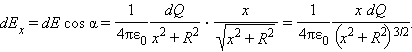
 |
При суммировании составляющих
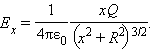
Суммирование составляющих
Обратите внимание, что на больших расстояниях, т. е. при
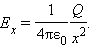
При
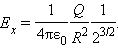
Это поле отличается от кулоновского поля, создаваемого точечным зарядом
 2 из 2
2 из 2
 |