 Модель 3.12.
Зоны Френеля
Модель 3.12.
Зоны Френеля Модель 3.12.
Зоны Френеля
Модель 3.12.
Зоны Френеля |
Одной из самых простых дифракционных задач является дифракция на круглых отверстиях или круглых дисках (шариках). Если точечный источник света и точка наблюдения находятся на оси системы, то задача просто решается методом зон Френеля. Радиусы кольцевых зон Френеля в плоскости препятствия в случае падения плоского волнового фронта определяются выражением
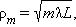 |
Если перекрыть непрозрачным экраном зоны Френеля через одну, то можно получить значительное усиление интенсивности колебаний в точке наблюдения, так как колебания только от четных (или только от нечетных) зон происходят в одной фазе. Такие устройства называют зонными пластинками Френеля. Они действуют подобно линзе.
При дифракции света на круглом диске в центре дифракционной картины всегда наблюдается светлое пятно (пятно Пуассона).
Общий вид дифракционной картины при дифракции света на круглых препятствиях достаточно сложен.
Для каждого положения точки наблюдения в стороне от оси симметрии результирующее колебание может быть найдено путем сложения колебаний от всех вторичных источников с учетом фазовых соотношений. Метод зон Френеля неприменим при нарушении осевой симметрии задачи. Определение результатов интерференции вторичных волн, в общем является сложной математической задачей, которая может быть решена с помощью компьютерного моделирования.
В данной компьютерной модели в нижнем левом окне изображены границы зон Френеля, определенные для точки наблюдения, находящейся на оси симметрии. Программа позволяет оставлять открытыми или закрывать непрозрачным экраном целые зоны Френеля. Для каждого случая компьютер рассчитывает дифракционную картину во всей плоскости наблюдения. Таким путем могут быть получены дифракционные картины при дифракции на зонных пластинках и продемонстрировано их фокусирующее действие.
Модель позволяет изменять длину волны
Обратите внимание, что если открыть только две соседние зоны, то в центре дифракционной картины возникает темное пятно. Если открыта только одна любая зона, то интенсивность колебаний в центре дифракционной картины в 4 раза превосходит



