
Учебник. Свободные колебания. Математический маятник
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = –mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
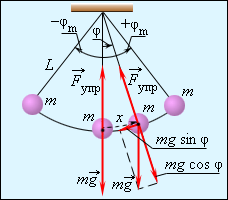
Если обозначить через x линейное смещение маятника от положения равновесия по дуге окружности радиуса l, то его угловое смещение будет равно φ = x / l. Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:
Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению x, а
Только в случае малых колебаний, когда приближенно можно заменить на математический маятник является гармоническим осциллятором, т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15–20°; при этом величина отличается от не более чем на 2 %. Колебания маятника при больших амплитудах не являются гармоническими.
Для малых колебаний математического маятника второй закон Ньютона записывается в виде
Таким образом, тангенциальное ускорение aτ маятника пропорционально его смещению x, взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:
Эта формула выражает собственную частоту малых колебаний математического маятника.
Следовательно,
Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали, проходящей через ось. При отклонении маятника на угол φ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:
Здесь d – расстояние между осью вращения и центром масс C.
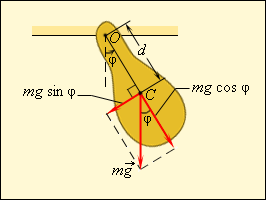
Знак «минус» в этой формуле, как обычно, означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент M пропорционален sin φ. Это означает, что только при малых углах φ, когда sin φ ≈ φ, физический маятник способен совершать свободные гармонические колебания. В случае малых колебаний
Здесь ω0 – собственная частота малых колебаний физического маятника.
Следовательно,
Более строгий вывод формул для ω0 и T можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение ε есть вторая производная углового смещения φ по времени:
Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде
Это уравнение свободных гармонических колебаний (см. уравнение (*) §2.2). Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.
По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции I можно выразить через момент инерции IC относительно оси, проходящей через центр масс C маятника и параллельной оси вращения:
Окончательно для круговой частоты ω0 свободных колебаний физического маятника получается выражение:
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ "Облако знаний".