

 |
 |
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка 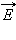 на площадь
на площадь 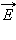 и нормалью
и нормалью 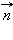 к площадке называется элементарным потоком вектора напряженности через площадку
к площадке называется элементарным потоком вектора напряженности через площадку
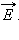
|
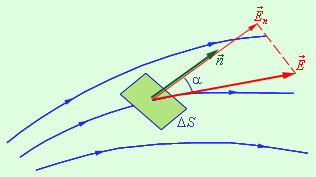
| Рисунок 1.3.1. К определению элементарного потока ΔΦ |
Рассмотрим теперь некоторую произвольную замкнутую поверхность 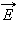 через эти малые площадки, а затем их просуммировать, то в результате мы получим поток
через эти малые площадки, а затем их просуммировать, то в результате мы получим поток 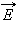 через замкнутую поверхность
через замкнутую поверхность
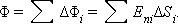 |
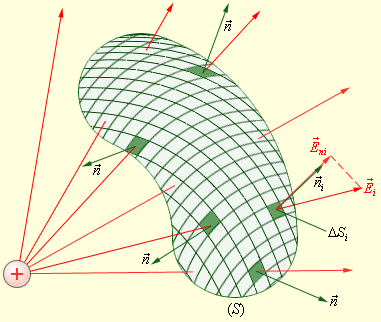
В случае замкнутой поверхности всегда выбирается внешняя нормаль.
|
| Рисунок 1.3.2. Вычисление потока Ф через произвольную замкнутую поверхность |
Поток вектора напряженности электростатического поля 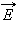 через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
|
Для доказательства рассмотрим сначала сферическую поверхность
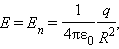 |
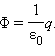
Окружим теперь точечный заряд произвольной замкнутой поверхностью
|
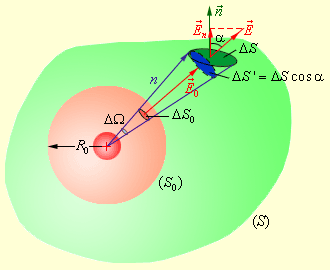
| Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность |
Рассмотрим конус с малым телесным углом
Здесь Δ
Так как
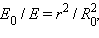 а
а 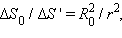 следовательно
следовательно 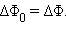 Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку
Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку
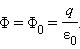 |
Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей 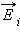 точечных зарядов. Поток
точечных зарядов. Поток 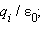 если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.
если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.
Таким образом, теорема Гаусса доказана.
Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.
Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.
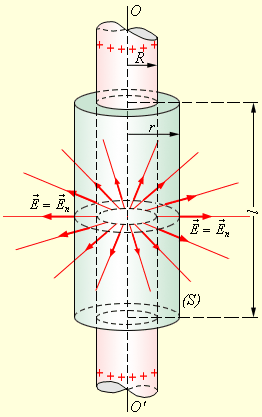
Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса
|
| Рисунок 1.3.4. Вычисление поля однородно заряженного цилиндра. |
При
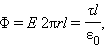 |
|
Этот результат не зависит от радиуса
Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая
Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.
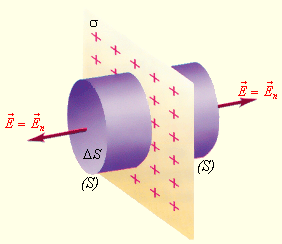
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).
|
| Рисунок 1.3.5. Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. |
В этом случае гауссову поверхность
|
Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.
 |
 |
 |

