

 |
 |
Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.
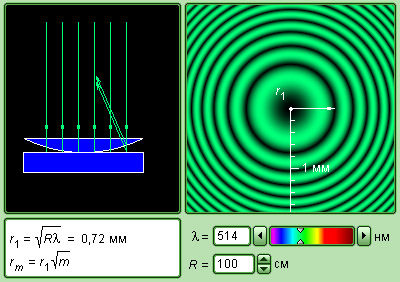
Первый эксперимент по наблюдению интерференции света в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 3.7.1). Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рис. 3.7.2).

|
| Рисунок 3.7.2. Кольца Ньютона в зеленом и красном свете |
Ньютон не смог с точки зрения корпускулярной теории объяснить, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов (см. § 3.6).
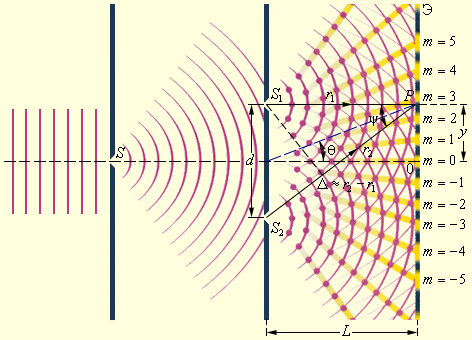
Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель
|
| Рисунок 3.7.3. Схема интерференционного опыта Юнга |
Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели
Монохроматическая (или синусоидальная) волна, распространяющаяся в направлении радиус-вектора 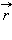 , записывается в виде
, записывается в виде
где
Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью:
Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке
|
(*) |
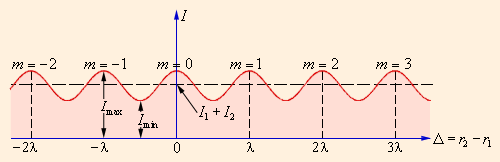
Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых
|
| Рисунок 3.7.4. Распределение интенсивности в интерференционной картине. Целое число |
В частности, если
|
|
(**) |
В этом случае
Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты.
Если в схеме Юнга через
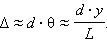 |
При смещении вдоль координатной оси
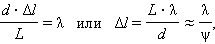 |
Следует подчеркнуть, что в волновой оптике, в отличие от геометрической оптики, понятие луча света утрачивает физический смысл. Термин «луч» употребляется здесь для краткости для обозначения направления распространения волны. В дальнейшем этот термин будет употребляться без кавычек.
В эксперименте Ньютона (рис. 3.7.1) при нормальном падении волны на плоскую поверхность линзы разность хода приблизительно равна удвоенной толщине
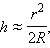 |
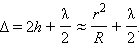 |
При
|
Эта формула позволяет экспериментально определить длину волны света
Проблема когерентности волн. Теория Юнга позволила объяснить интерференционные явления, возникающие при сложении двух монохроматических волн одной и той же частоты. Однако повседневный опыт учит, что интерференцию света в действительности наблюдать не просто. Если в комнате горят две одинаковые лампочки, то в любой точке складываются интенсивности света и никакой интерференции не наблюдается. Возникает вопрос, в каких случаях нужно складывать напряженности (с учетом фазовых соотношений), в каких – интенсивности волн, т. е. квадраты напряженностей полей? Теория интерференции монохроматических волн не может дать ответа на этот вопрос.
Реальные световые волны не являются строго монохроматическими. В силу фундаментальных физических причин излучение всегда имеет статистический (или случайный) характер. Атомы светового источника излучают независимо друг от друга в случайные моменты времени, и излучение каждого атома длится очень короткое время
Интерференция может возникнуть только при сложении когерентных колебаний, т. е. колебаний, относящихся к одному и тому же цугу. Хотя фазы каждого из этих колебаний также подвержены случайным изменениям во времени, но эти изменения одинаковы, поэтому разность фаз когерентных колебаний остается постоянной. В этом случае наблюдается устойчивая интерференционная картина и, следовательно, выполняется принцип суперпозиции полей. При сложении некогерентных колебаний разность фаз оказывается случайной функцией времени. Интерференционные полосы испытывают беспорядочные перемещения из стороны в сторону, и за время
Таким образом, интерференция может возникнуть только при сложении когерентных колебаний. Волны, создающие в точке наблюдения когерентные колебания, также называются когерентными. Волны от двух независимых источников некогерентны и не могут дать интерференции. Т. Юнг интуитивно угадал, что для получения интерференции света нужно волну от источника разделить на две когерентные волны и затем наблюдать на экране результат их сложения. Так делается во всех интерференционных схемах. Однако, даже в этом случае интерференционная картина исчезает, если разность хода

 |
|
Модель.
Кольца Ньютона
|

 |
|
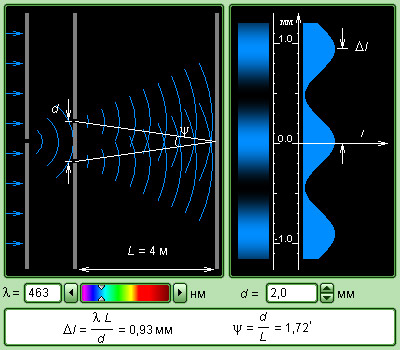
Модель.
Интерференционный опыт Юнга
|
 |
 |
 |

