

 |
 |
При выполнении любых физических измерений исключительную роль играют пространственно-временные соотношения между событиями. В СТО событие определяется как физическое явление, происходящее в какой-либо точке пространства в некоторый момент времени в избранной системе отсчета. Таким образом, чтобы полностью охарактеризовать событие, требуется не только выяснить его физическое содержание, но и определить его место и время. Для этого необходимо использовать процедуры измерения расстояний и промежутков времени. Эйнштейн показал, что эти процедуры нуждаются в строгом определении.
Для того чтобы в выбранной системе отсчета выполнять измерения промежутка времени между двумя событиями (например, началом и концом какого-либо процесса), происходящими в одной и той же точке пространства, достаточно иметь эталонные часы. Наибольшей точностью в настоящее время обладают часы, основанные на использовании собственных колебаний молекул аммиака (молекулярные часы) или атомов цезия (атомные часы). Измерение промежутка времени опирается на понятие одновременности: длительность какого-либо процесса определяется путем сравнения с промежутком времени, отделяющим показание часов, одновременное с концом процесса, от показания тех же часов, одновременного с началом процесса. Если же оба события происходят в разных точках системы отсчета, то для измерения промежутков времени между ними в этих точках необходимо иметь синхронизованные часы.
Эйнштейновское определение процедуры синхронизации часов основано на независимости скорости света в пустоте от направления распространения. Пусть из точки
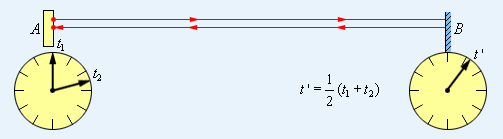
|
| Рисунок 4.2.1. Синхронизация часов в СТО |
Существование единого мирового времени, не зависящего от системы отсчета, которое принималось как очевидный факт в классической физике, эквивалентно неявному допущению о возможности синхронизации часов с помощью сигнала, распространяющегося с бесконечно большой скоростью.
Итак, в разных точках выбранной системы отсчета можно расположить синхронизованные часы. Теперь можно дать определение понятия одновременности событий, происходящих в пространственно-разобщенных точках: эти события одновременны, если синхронизованные часы показывают одинаковое время.
Рассмотрим теперь вторую инерциальную систему
Пусть оба события в системе
Для ответа на этот вопрос рассмотрим следующий мысленный эксперимент. На одном конце твердого стержня некоторой длины
В системе
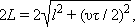 |
Из этих соотношений можно найти связь между
|
Таким образом, промежуток времени между двумя событиями зависит от системы отсчета, т. е. является относительным. Собственное время
Эффект замедления времени является взаимным, в согласии с постулатом о равноправии инерциальных систем 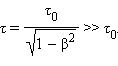 , так как
, так как
С релятивистским эффектом замедления времени связан так называемый «парадокс близнецов». Предполагается, что один из близнецов остается на Земле, а второй отправляется в длительное космическое путешествие с субсветовой скоростью. С точки зрения земного наблюдателя, время в космическом корабле течет медленнее, и когда астронавт возвратится на Землю, он окажется гораздо моложе своего брата-близнеца, оставшегося на Земле. Парадокс заключается в том, что подобное заключение может сделать и второй из близнецов, отправляющийся в космическое путешествие. Для него медленнее течет время на Земле, и он может ожидать, что по возвращению после длительного путешествия на Землю он обнаружит, что его брат-близнец, оставшийся на Земле, гораздо моложе его.
Чтобы разрешить «парадокс близнецов», следует принять во внимание неравноправие систем отсчета, в которых находятся оба брата-близнеца. Первый из них, оставшийся на Земле, все время находится в инерциальной системе отсчета, тогда как система отсчета, связанная с космическим кораблем, принципиально неинерциальная. Космический корабль испытывает ускорения при разгоне во время старта, при изменении направления движения в дальней точке траектории и при торможении перед посадкой на Землю. Поэтому заключение брата-астронавта неверно. СТО предсказывает, что при возвращении на Землю он действительно окажется моложе своего брата, оставшегося на Земле.
Эффекты замедления времени пренебрежимо малы, если скорость космического корабля гораздо меньше скорости света
В настоящее время уже необходимо принимать во внимание релятивистский эффект замедления хода часов при транспортировке атомных часов на большие расстояния.

 |
|
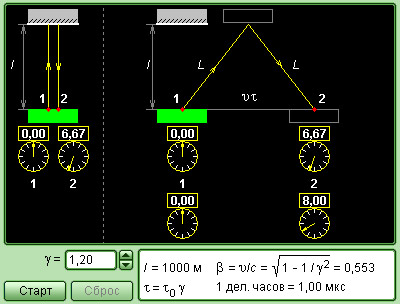
Модель.
Относительность промежутков времени
|
 |
 |
 |

